写在前面
- 此文是我入门AI的学习笔记,教材是《nueral networks and deep learning》,作者Michael Nielsen。
- 这是一本免费的书籍,网址在这里.
- 此文是对书中第四章内容的整理归纳和分析,关于前几章的知识点,在我之前的博客之中。
- 初学者入门,可能会有错误,请大家批评指正。
本次的内容主要是为了证明一个问题,即神经网络可以用来计算任何一个函数。
这是一种普遍性的解释
This result tells us that neural networks have a kind of universality. No matter what function we want to compute, we know that there is a neural network which can do the job.
在此次的证明中,我们忽略了函数本身的数学性质,而是从图形的角度出发,用一种直观、形象、可视化的方式证明了这个普遍性。
两个预先声明
在进行证明之前,有两点预先声明需要澄清
- 神经网络给出的并不是函数的精确值,而是一个近似估计(approximation)。
- 我们进行预估的函数必须是连续函数,非连续函数是无法使用神经网络进行估计的。(因为原本我们的神经网络对于输入是进行连续型的计算)
对于第二个问题,一般来说我们也可以用连续的函数去拟合非连续的函数,最终得到的效果也很不错,所以在实践中并不是什么严重的限制。
一个输入和一个输出的情况
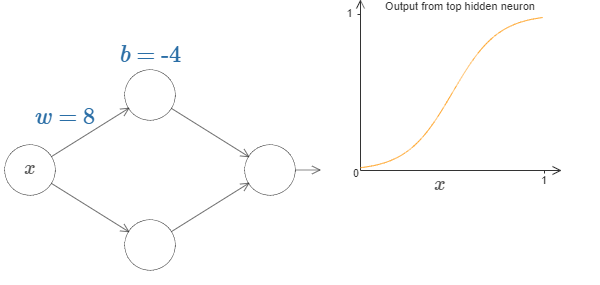
注:此处使用的神经元是s型神经元。
在上图所示的具有单个输入和单个输出的神经网络中,我们将隐藏层的底层神经元的权值设为0,而关注顶层神经元。当改变权值w和偏置b时,我们得到的输出图形会发生变化。演示网页
最后得出的结论是:改变权值会改变图像的陡峭程度,改变偏置会改变图像的左右位置
而我们将权重w设置的很大时,图像图像就变成了阶跃函数(step function)。
由计算(附后)可以得到,阶跃点x的坐标为-b/w
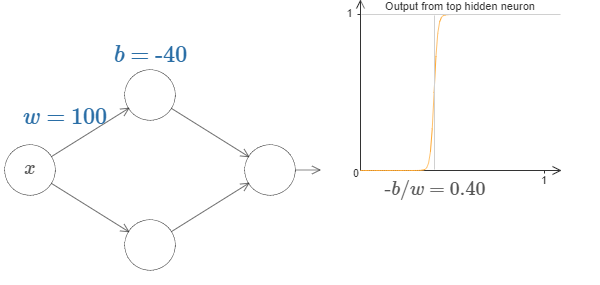
我们用字母s来表示阶跃点的位置,即
1 | s=-b/w |
接下来我们加入底层神经元,一起来探究图形的变化。
根据上面的经验我们可以得到,当我们将底层神经元的权重也设置的很大时,图像将会得到两个阶跃,其中s1,s2分别代表了两个阶跃点的坐标。
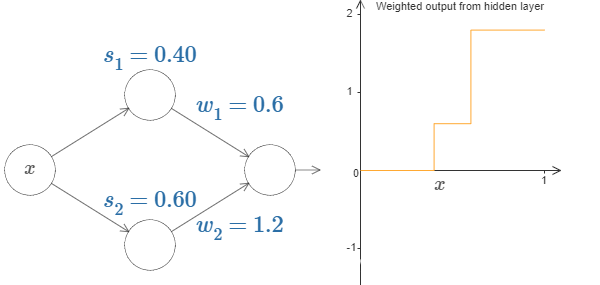
而上图中,由图形演示我们可以知道,w1和w2分别控制了两个阶跃点的高度。
当我们将两个阶跃点的高度设置正好互为相反数时,就可以得到一个凸起(bump)。如下图所演示。
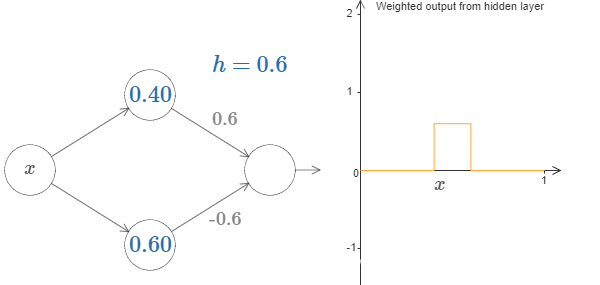
我们用h来表示凸起的高度,即
1 | h=w1=-w2 |
当我们用编程的角度去看待这个问题,就可以得到一个if-then-else的陈述。
1 | if input>step point |
当隐藏层只有两个神经元时,我们可以得到一个一个凸起。由此可知,当我们在隐藏层加入更多的神经元,就可以得到不同位置,不同高度的凸起。
两对时:
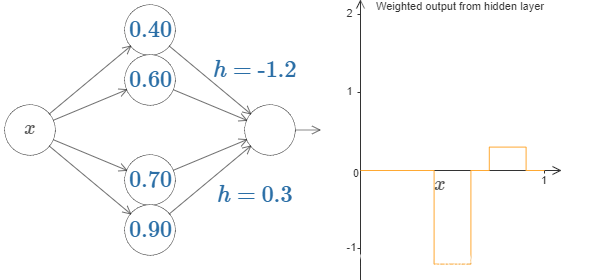
让我们去尝试拟合一个复杂的一元函数
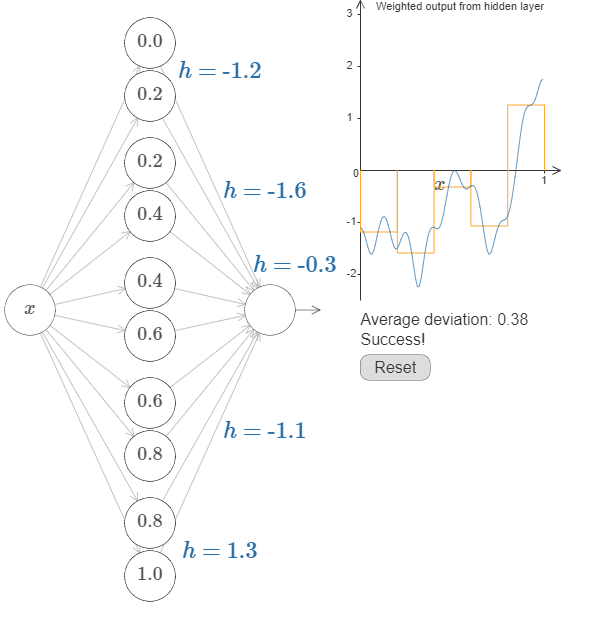
上图所示的演示使用了五对隐藏神经元 ,对一个复杂函数图像的模拟虽然不是特别的精确,但是它告诉我们了精确模拟的可能性,即添加更多的隐藏神经元,改变他们的阶跃点和高度,最终将会得到偏差很小的模拟。
两个输入的情况
如图,我们将两个输入分别设为x和y,它模拟的是二元函数的情况。
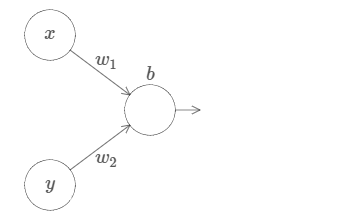
为了方便思考,我们先将y的输入权值设为0,即w2=0,而考虑x轴的情况。
有了前面单个输入的经验,我们可以知道,当w1很大的时候,函数图像再次出现阶跃现象。
我们也可以用同样的方法,在x轴方向得到凸起。
如上图所示。此时y输入指向隐藏神经元的权重均为0.
参数解释:
- x 0.3:第一个阶跃点的位置是x=0.3
- x 0.7:第二个阶跃点的位置是x=0.7
- h:凸起的高度,也是隐藏神经元的输出权重。
同样的图形也可以在y轴方向演示。
此时x输入指向隐藏神经元的权重均为0.
此时我们将x、y方向进行叠加,得到如图所示的函数图像。
此时,四周“高原”的高度为h,中间“塔”的高度为2h。
为了得到与单个神经元“凸起”相似的结构,我们需要对输出层的偏置进行合理的选择。
数学计算(附后)与实际图像操作告诉我们,当偏置b的值设定为-3/2h时,会得到中间凸起的塔形函数。
增加隐藏神经元的数量,即可得到不同高度,不同位置的塔,从而对不同的二元函数进行拟合计算。
如下图所示,两个塔的情况。
其中第三层w的值用来控制塔的高度
以及很多塔的情况

多个输入的情况
根据以上的经验,我们可以得出,对于多个输入的神经网络拟合情况。
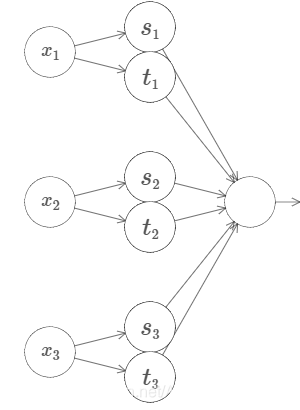
- 第一层权值设置的很大,同时调整偏置,得到类似“阶跃”结构。
- 第二层权值 交替设置为+h,-h,设置偏置为(-m+0.5)h ,其中m为输入的个数。
- 第三层的权值设置用来控制高度,,设置偏置使其满足σ^-1^◦f 的函数图像。
S型神经元的延伸
以上结论都是在s型神经元的基础上得来的。
如下图是s型神经元的输出函数图。
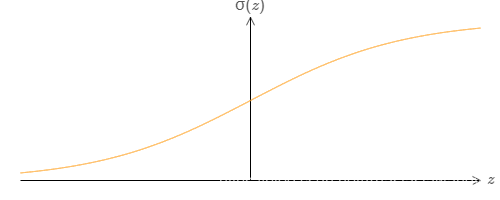
但是这个结论是可以推广到更多的神经元模型上。
如下图,激活函数的图形是不规则的形状。
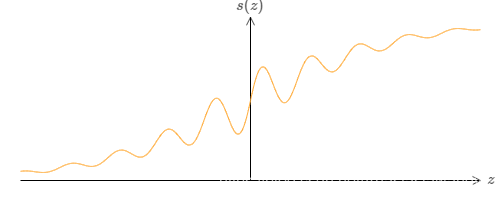
当我们按照上面的方法,将权值增大,同时调整偏置时,依旧可以得到一个很好的阶跃函数,其中阶跃点的值为-b/w。演示网页

因此我们可以使用这个神经元模型,通过上述所得的技巧来完成对所给函数的拟合。
但是并非所有的激活函数都可以用来拟合,事实上,函数需要满足条件
- z→−∞和z→∞ 时,函数的值是确定的,也就是我们阶跃函数所取的两个值。
- 上述两个值不能相同。
修补阶跃函数
此处关注的是,我们在用阶跃函数拟合真实函数时,出现的故障窗口(window of failure)
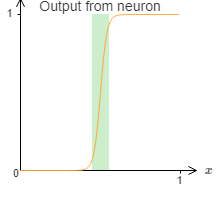
当然我们可以通过增大权值来使此窗口变得很窄,但是这里作者给出了另一个解决办法。
假设我们隐藏神经元的加权输出σ^-1^◦f 图像为
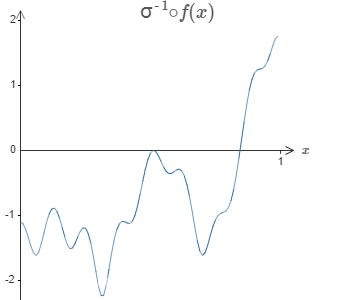
我们采用一个输入,一个输出的方式得到了如下图所示的拟合。
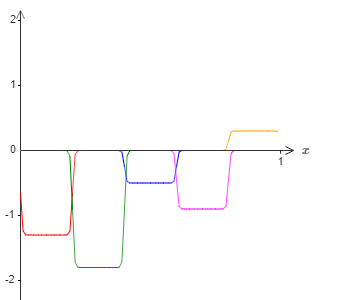
我们将上图的凸起高度减半,得到下图。
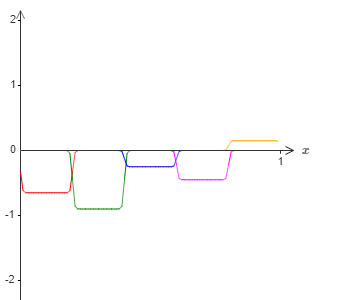
第二个操作是,将上述图像向右平移,平移的距离是阶跃长度的一半,得到的图像如下。
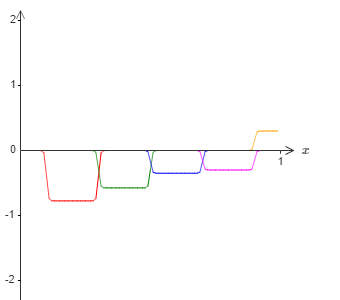
将上述两个图像叠加,得到的这个整体的近似仍然在⼀些⼩窗⼝的地⽅有故障。但是问题⽐以前要小很多。原因是在⼀个近似中的故障窗⼝的点,不会在另⼀个的故障窗⼝中。
我们甚⾄能通过加⼊更多的平移结果,⽤ M 表⽰,重叠的近似 σ^-1^◦f/M 来做得更好。假设故障窗⼝已经⾜够窄了,其中的点只会在⼀个故障窗⼝中。并且假设我们使⽤⼀个 M ⾜够⼤的重叠近似,结果会是⼀个⾮常好的整体近似。
结论
- 此章的内容是用可视化的方式,证明了神经网络可以用来拟合计算任意一个函数。
- 此章对于普遍性的解释当然不是如何使⽤神经⽹络计算的切实可⾏的⽤法,但是理解此章的内容依旧十分重要。
- 正是因为任意函数都是可以用神经网络来拟合计算的,因此真正重要的问题不是这个函数是否存在,而是找到一个好的计算函数的方法。
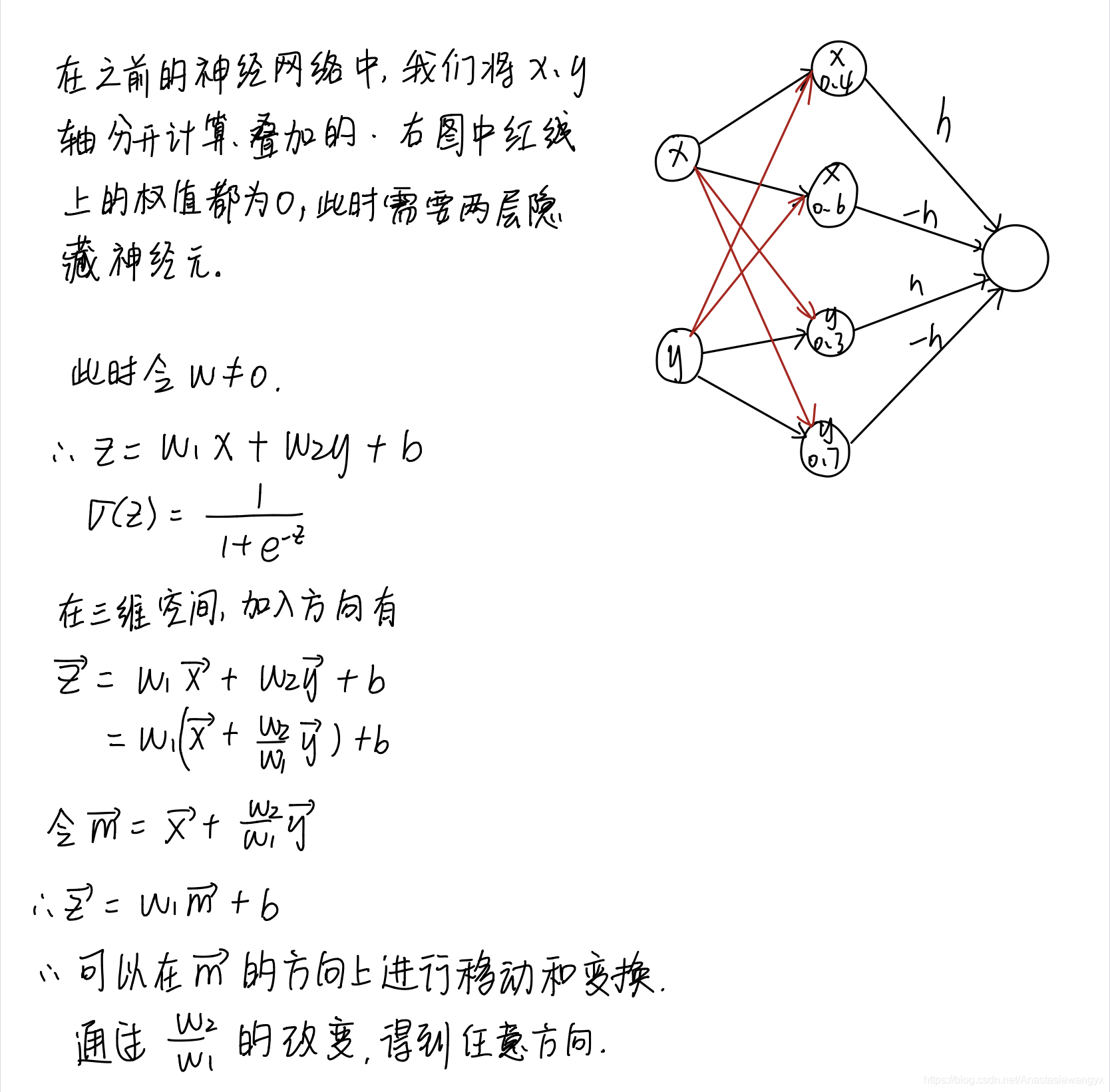
证明题
- 阶跃点的位置(以一个输入和一个输出的情况为例)
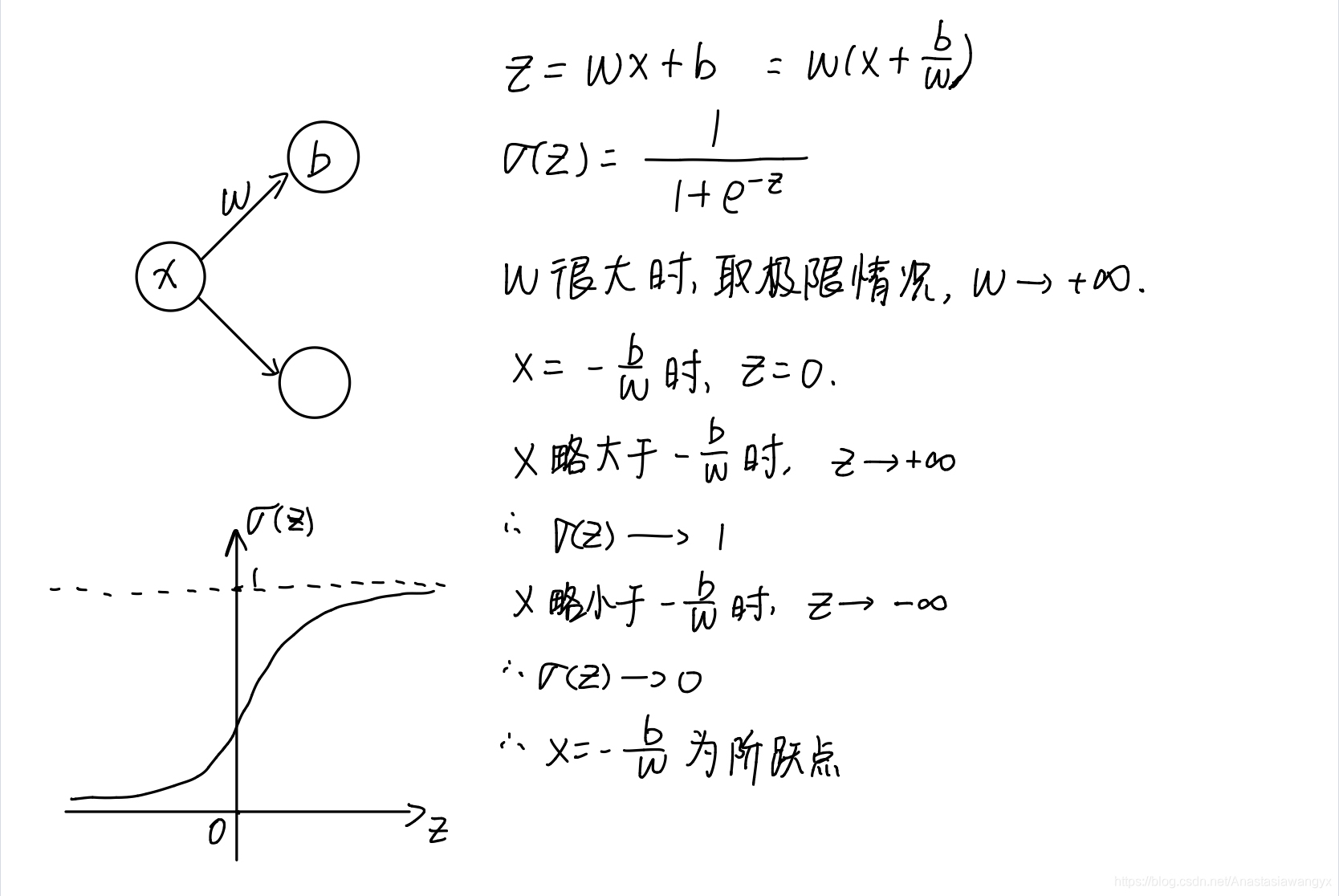
- 证明中间凸起的塔形函数的偏置b的值设定为(-m+0.5)h,其中m为输入的个数。

- 证明对于两个至多个的情况,上述情况所使用的两层隐藏神经元的情况可以减少为使用单层隐藏神经元。